
| HOME | MENU | DOCS | SEARCH |
All the known optical phenomenon in the atmosphere (see the Atmosphere); it is observed when the sun lights a veil of the falling rain and the observer is between the sun and a rain. The phenomenon it is presented in the form of one, is more rare — two concentric light arches which are drawn in a firmament from the falling rain and "iridescent" flowers painted concentric in a row. The internal, most often visible arch is painted from the outer edge in red color, from the internal — in violet; between them regularly a solar range (see) colors lie: (red), orange, yellow, green, blue and violet. The second, less often an observed arch lies over the first, is painted ordinary more poorly, and an order of an arrangement of flowers in it the return. The part of a firmament in the first arch seems ordinary very light, the part of a firmament over the second arch seems to less light, the ring space between arches seems dark. Sometimes, except these two main elements of a rainbow, still the additional arches representing the weak color indistinct strips bordering the top part of an inner edge of the first rainbow less often — the top part of an outer edge of the second rainbow are observed.

Sometimes, very seldom, the rainbow is observed in the same conditions and at illumination of a rain cloud by the moon. The same phenomenon of a rainbow is noticed sometimes and when lighting by the sun of the water dust which is in the air near the fountain or falls. When the sun is closed by easy clouds — the first rainbow seems sometimes absolutely not painted and the firmament background is presented in the form of a whitish arch, by lighter, than; such rainbow call white.
Supervision of the phenomenon of a rainbow showed that arches represent it the correct parts of circles which center lies always on the line passing through the head of the observer and the sun; as thus the center of a rainbow at highly standing sun lies below the horizon, the observer sees only small part of an arch; at a decline and sunrise when the sun on the horizon, the rainbow is presented in the circle semi-arch form. From top of very high mountains, from a balloon it is possible to see a rainbow and in the form of the most part of an arch of a circle as under these conditions the center of a rainbow is located over the visible horizon.

Supervision over a rainbow showed that the corner formed by two lines which are mentally carried out from the observer's eyes to the center of an arch of a rainbow and to its circle, or the angular radius of a rainbow is size approximately constant and equal for the first rainbow about 41 °, for the second 52 °. The elementary explanation of the phenomenon of a rainbow was offered in 1611 A. De-Domini in his composition of "De Radiis Visus et Lucis", developed then Descartes ("Les meteores", 1637) and quite developed by Newton in his "Optics" (1750). According to this explanation the phenomenon of a rainbow occurs owing to refraction and full internal reflection (see Dioptrics) sunshine in rain drops. If SA beam, it (figs falls to a spherical drop of liquid. 1), having undergone refraction in the AVATARS direction, it can be reflected from a back surface of a drop in the VS direction and to leave, having again refracted, in the CD direction.

Figs. 1.
The beam which differently fell to a drop, maybe, however in a point With (figs. 2) the second time to be reflected on CD and to leave, having refracted, in the DE direction.

Figs. 2.
If not one beam, but the whole bunch of parallel beams falls to a drop, how it is proved in optics, all beams, preterpvshy one internal reflection in a water drop, will leave a drop in the form of the dispersing cone of beams (figs. 3), which axis is located in the direction of the falling beams [Actually the bunch of the beams leaving a drop doesn't represent the correct cone, and even everything the beams making it aren't crossed in one point, only for simplicity on the following drawings these bunches are taken for the correct cones with top in the center of a drop.].
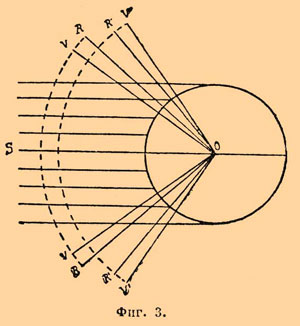
Figs. 3.
The corner of an opening of a cone depends on index of refraction (see Dioptrics) liquids and as the index of refraction isn't identical to the beams of various color (various wavelength) making a white ray of sunlight, and the corner of an opening of a cone will be various for beams of different color, for violet will be less, than for red. Thereof the cone will be bordered with color iridescent edge, red from the outside, violet inside, and if a drop water, a half of an angular opening of a cone of SOR for red color is about 42 °, for violet (SOV) 40,5 °. Research of distribution of light in a cone shows that almost whole world is concentrated in this color border of a cone and is extremely weak in the central parts it; thus we can consider only a bright color cover of a cone as its all internal beams are too weak to be apprehended the zrniy.

Similar research of the beams twice reflected in a water drop will show us that they will leave the same conic iris of the eye of V'R' (figs. 3), but red from an inner edge, violet with external, and for a water drop a half of an angular opening of the second cone will be equal 50 ° for red (SOR') and 54 ° for the violet edge (SOV).
We will imagine now that the observer which eye is in a point About (figs. 4), looks at a number of vertical rain drops of A, B, C, D, E..., lit with the parallel sunshine going in the SA, SB, SC direction etc.; let all these drops be located in the plane passing through an eye of the observer and the sun; each such drop will be, on previous, to radiate two conic light covers which general axis will be a ray of sunlight falling on a drop.
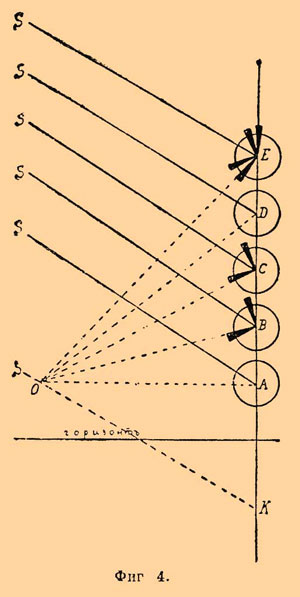
Figs. 4.
Let the drop In be located so that one of the beams forming an internal cover of the first (internal) cone at continuation will pass through the observer's eye; then the observer will see in In a violet point. Slightly higher than a drop In such drop will be located With that the beam going from an external surface of a cover of the first cone will get to an eye and will give in it impression of a red point in With; drops, intermediate between In and With, will give in an eye impression of points blue, green, yellow and orange. In the sum — an eye will see in this plane the vertical iridescent line with the violet end below and red above; if we carry out through About and the sun the SO line, the corner formed by it with the OV line will be equal to a semi-opening of the first cone for violet beams, i.e. 40,5°, and the corner of BRAIDS will be equal to a semi-opening of the first cone for red beams, i.e. 42°. If to turn KOV corner round OK, OB will describe a conic surface and each drop lying on a circle of crossing of this surface with a rain veil will give impression of a light violet point, and all points together will give a violet arch of a circle with the center in To; it is in the same way formed red and intermediate arches, and in the sum of eyes will receive impression of a light iridescent arch, violet inside, red from the outside — the first rainbow.

Having put the same reasonings to the second external light conic cover radiated by drops and formed by sunshine, twice in a drop reflected, we will receive wider second concentric rainbow with a corner, WHICH, equal for inner red edge — 50°, and for external violet — 54°. Owing to double reflection of light in the drops giving this second rainbow it will be much less bright, than the first. The drops of D lying between C and E don't radiate light at all in an eye and therefore the space between two rainbows will seem dark; from the drops lying below In and higher than E the white beams proceeding from the central parts of cones and therefore the very weak will get to an eye; it explains why the space under the first and over the second rainbow seems to us poorly lit.
Unsharpness and blurring of paints of a rainbow is explained by that a source of lighting is not the point, but the whole surface — the sun and that the separate sharper rainbows formed by separate points of the sun are imposed at each other. If the sun shines through a veil of thin clouds, the shining source is the cloud surrounding the sun throughout 2 — 3° and separate color strips are so imposed at each other that an eye doesn't distinguish flowers any more, and sees only a colourless light arch — a white rainbow.

The stated theory foretells further that some beams in water drops undergo 3-4-5-fold reflection more and leave a drop the iridescent conic covers forming a rainbow the third, fourth, fifth etc. or as speak, a rainbow of the highest orders. Research shows, however, that cones of a rainbow of the third and fourth order are directed by openings from the sun; these rainbows would be visible to the observer looking through a rain veil at the sun if dazzling light of the last didn't interfere to notice them. The rainbow of the fifth order is directed the same as a rainbow of the first and second, and has angular radius in 55 °; it, apparently, however, was never observed because of extreme weakness of light radiated by it.
Miller, Pulfrikh, Bilye and friend. studied the artificial rainbows received at supervision of reflection and light refraction in a cylindrical stream of the water lit by the source placed for the observer and under these conditions could notice rainbows to 19 about; the angular radiuses of rainbows measured by them are very close to predicted by the theory. The stated elementary theory of rainbows has to be considered, however, only as the first approach to the true theory of a rainbow as she doesn't find out emergence of additional rainbows and as the angular radiuses of rainbows predicted by it it is slightly more observed (the first rainbows with corners from 38° to 40° were observed).
Jung, Potter and then, in particular Erie (1838 — 48), developed more perfect theory of a rainbow based on consideration of the phenomena of diffraction (see) at refraction and reflection of light in water drops. This theory very difficult and not giving in to an elementary statement, quite explains all features of a rainbow, and also emergence of additional rainbows. According to this theory, angular radiuses of additional rainbows depend on the size of drops and these rainbows are more visible to those, than it is less than drop.

As rain drops increase as approaching the earth, additional rainbows can be well seen only at refraction and reflection of light in highly located layers of a rain veil, i.e. with a small height of the sun and only at the top parts of the first and second rainbow. The complete theory of a white rainbow was given by Pertner in 1897. The question of was often started, whether various observers see the same rainbow and whether the rainbow seen in a silent mirror of the big water tank, reflection of directly observed rainbow represents.
The elementary theory of a rainbow obviously specifies that various observers see the rainbows formed by various drops of a rain, i.e. different rainbows, and that the seeming reflection of a rainbow is that rainbow which would be seen by the observer placed under the reflecting surface at such distance from it down on what it is over it. The excentric rainbows observed in rare instances, in particular at the sea, crossed are explained by reflection of light from a surface of the water behind the back of the observer and emergence, thus, of two light sources (the sun and its reflection) giving everyone the rainbow.
Subuniforms. see Airy, "Transactions of the C ambridge Philosophical Society" (t. VI, 1838); Perntner, "Sitzungsb. d. Wiener Akademie" (t. 106, 1897), and also Mascart, "Traite d'Optique" (t. I, p. 382 — 405).

When writing this text material was used from
Encyclopedic dictionary of Brockhaus F.A. and Efron I.A. (1890 — 1907).
<< Back: The general list of the terms connected with weather
We recommend that you look at the popular sections of the site myvaleology.com: MENU with a description of the sections | |||
| SOCIAL | DONATION | MY DIET | MY SPORT |

|
Release all4e8 |
||
Copyright © VZOJ 2023. All rights reserved. When reprinting or quoting myvaleology.com materials please put a link to the site myvaleology.com :
<a href="https://myvaleology.com">Healthy lifestyle</a>