
| ДОМ | МЕНЮ | ДОКИ | ПОИСК |
(франц. marées, нем. Gezeiten, англ. tides) — периодические колебания уровня воды вследствие притяжения Луны и Солнца.
Общие сведения. Приливы всего заметнее по берегам океанов. Тотчас после малой воды — наибольшего отлива, уровень океана начинает повышаться, вода заливает берег, сначала медленно, затем все быстрее и быстрее; после среднего положения уровня быстрота поднятия уменьшается. Наступает полная вода — наибольший прилив, и сейчас же начинается убыль, вначале медленная, проходит с наибольшей быстротой средний уровень и, снова замедляясь, достигает отлива. В открытом океане приливы совершенно незаметны, так как не с чем сравнивать положение уровня, а горизонтальные передвижения воды ничтожны. Каждая убыль и прибыль воды длится около 6 часов; явление повторяется средним числом через 12 h25m; каждый день бывает два прилива, причем они, запаздывая ежедневно на 50 m, последовательно приходятся на различное время суток.
Период в 24 h50m равен лунным суткам — промежутку, в который Луна в своем видимом движении совершает полный круг около Земли. Это указывает, что приливы главным образом зависят от Луны. Прилив для данной местности Земли наступает, когда Луна находится приблизительно в одной и той же стороне неба. Промежуток времени между прохождением Луны через меридиан и приливом несколько меняется в зависимости от фаз Луны. Его величина для прилива, ближайших к полнолунию или новолунию (сизигиям), называется прикладным часом (é tablissement du port, Hafenzeit, establishment). Прикладные часы различных, иногда очень близких, мест весьма отличаются друг от друга. Так как в сизигиях Луна проходит меридиан в полдень или в полночь, прикладной час есть момент прилива в дни полнолуния или новолуния по местному времени.

Причина приливов. Луна притягивает не одинаково различные точки Земли: частицы, ближайшие к ней, — всего сильнее, центр Земли — слабее, противоположные части — еще слабее. Если ρ — радиус Земли, R — расстояние ее до Луны, M — масса Луны, κ — коэффициент притяжения (см. Тяготение), приближенная разность сил, действующих на центр и на одну из крайних точек, равна 2 κ M ρ /R3. Разность притяжений Луны называется приливной силой; она изменяется с зенитным расстоянием Луны. В точках Земли, где Луна приходится в зените или надире, приливная сила уменьшает тяжесть; там, где Луна в горизонте, — увеличивает тяжесть; в промежуточных точках — частью изменяет тяжесть, частью направлена горизонтально.
Полное действие приливной силы Луны равно 1/9000000 земного притяжения (около 0,1 мг на 1 кг). Обнаружить ее непосредственно почти невозможно, так как случайные местные изменения тяжести и уклонения отвеса значительно больше, но ее действие сказывается на деформации всей фигуры Земли. Частицы, ближайшие к Луне, стремятся к ней больше, чем центр Земли, а частицы удаленные как бы отстают от центра в этом стремлении, и таким образом получаются две выпуклости или волны, одна обращенная к Луне, другая — в противоположную сторону. Если бы Земля была сплошь покрыта океаном и не имела бы вращения вокруг оси, то она приняла бы форму вытянутого эллипсоида вращения с наибольшей осью, направленной к Луне. Было бы два неизменных прилива высотой около 2/3 м, разделенных кольцом отлива. Вследствие вращения Земли приливная сила Луны действует постоянно на новые точки Земли.
Раз образовавшаяся волна могла бы по законам движения жидкостей неотступно следить за светилом, то есть двигаться с востока на запад (против вращения Земли) со скоростью 1600 км в час, только при глубине океана в 20 км. Если глубина меньше, что и соответствует действительности, волны должны отставать. Притяжение Луны возбудит новые и новые волны, налегающие одна на другую, и таким образом появится составная волна, следующая за Луной. Уже из этого видно, что прилив не происходит непременно в точках Земли — ближайшей и противоположной Луне. При некоторых условиях глубины (см. ниже) в этих точках будет отлив, и Земля представит собой сжатый эллипсоид вращения. Континенты, мешающие свободному движению волн, извилины берегов, внутреннее трение жидкости, неровности дна океана и т. д. искажают явление прилива и делают его в деталях недоступным теории, но период волны остается неизменным и тем указывает на конечную причину явления.

Подобные же волны производятся Солнцем. Масса Солнца компенсируется громадным расстоянием, и его приливная сила приблизительно в 2,2 раза меньше лунной, составляет 1/20000000 земного притяжения. Солнечный прилив вследствие его малости не замечается отдельно, но только видоизменяет лунный. В моменты сизигий Солнце и Луна находятся на одной линии с Землей, приливная сила их направлена одинаково, поэтому приливные водны совпадают и сизигийные приливы — сумма лунного и солнечного. Во время же Квадратур, т. е. первой или последней четверти, Солнце и Луна видимы с Земли под углом в 90° между ними, солнечный прилив совпадает с лунным отливом и квадратурные приливы равны разности лунного и солнечного. В остальное время величина прилива колеблется между этими крайними значениями. Все это носит название месячного неравенства. В течение каждого лунного месяца наступают два раза большие сизигийные приливы и два раза малые — квадратурные (eaux vives и eaux mortes, Springzeit и taube Gezeit, springtide и neaptide). Месячное неравенство влияет также на время прилива. После новолуния до первой четверти Солнце проходит немного раньше Луны через меридиан места, и поэтому составной прилив наступает раньше лунного. Между первой четвертью и полнолунием солнечный прилив уже ближе к предыдущему лунному, потому влияет на него и производит опаздывание составного прилива.
Точно так же прилив наступает раньше от полнолуния до последней четверти и запаздывает от последней четверти до новолуния. Эта поправка прикладного часа бывает очень значительной — больше часа. Теоретическое отношение приливных сил Солнца и Луны 4:9, отсюда отношение сизигийных и квадратурных приливов 13:5. Промежутки от кульминаций Луны и Солнца до соответственных приливов иногда различаются между собой, поэтому оба прилива в дни сизигий, когда Луна и Солнце одновременно проходят через меридиан, могут не вполне совпадать, а наибольший прилив приходится не в самый день сизигии. Например, если для лунного прилива промежуток меньше на 1,25 h, то наибольший прилив наступит, когда Солнце в видимом движении уйдет вперед Луны на 1,25 h, то есть через полтора дня после сизигии, что и наблюдается во многих портах Западной Европы.
Это явление называется — возраст прилива. Исправленный прикладной час относится к наибольшему приливу. Когда возмущающее светило (Солнце или Луна) находится в экваторе, приливные волны располагаются симметрично на земном шаре относительно полюсов и оба прилива суток равны между собой; эта симметрия нарушается, если светило имеет значительное склонение. Если широта места и склонение светила одноименны (обе северные или обе южные) наибольший прилив наступает при верхней кульминации; если разноименны — при нижней. Это называется суточным неравенством.

В европейских портах оно почти незаметно, но в некоторых местностях так велико, что наблюдается в сутки один прилив и один отлив, разделенные промежутком в 12 h25m. Склонение светил влияет на величину сизигийных приливов. Равноденственные сизигийные приливы — наибольшие в году. Склонение Луны изменяется между крайними пределами в течение лунного месяца. Следствием этого является неравенство в приливах с периодом в 27 дней. Аналогичное солнечное неравенство имеет периодом год. Смотря по положению узлов лунной орбиты на эклиптике (см. Луна, Узел), склонение Луны может достигать то 28°, то только 18°, поэтому движение узлов производит новое неравенство с периодом в 18,7 лет. Изменение расстояния светил очень сказывается на размерах прилива. Эксцентриситет орбиты Луны значителен, поэтому прилив в апогее гораздо меньше, чем в перигее; отношение их достигает 2:3. Наконец, на прилив имеют влияние главнейшие возмущения в движении Луны: эвекция, вариация (см.). Все эти неравенства вместе носят название неравенств долгого периода.
История вопроса. Приливы и их связь с Луной были известны в глубокой древности китайцам. Греки имели мало сведений о приливах, так как в Средиземном море они ничтожны. Геродот упоминает о приливах Красного моря, как необыкновенно больших. Римляне познакомились с приливами Атлантического океана, и тогда же была окончательно установлена связь с Луной и ее фазами. Цезарь упоминает: был большой прилив, так как наступило полнолуние. Подобные же указания встречаются у Посидония, Плиния и Страбона.
В начале средних веков Бэда говорит уже о различии прикладных часов и о том, что приливные волны распространяются по восточному берегу Англии с севера на юг. Древние отчаялись дать какое-либо объяснение приливам и даже назвали их могилой человеческого любопытства. Декарт пытался объяснить на основании своей теории вихрей. Кеплер первый утверждал, что приливы — следствие притяжения Луны и что, не существуй на Земле тяжести, океаны устремились бы на Луну. Странно, что Галилей счел это печальным возвращением в область мистических бредней и предпочитал объяснять вращением Земли.

Ньютон, сформулировав закон притяжения, вполне выяснил истинную причину явления. Теория Ньютона, изложенная в его "Principia", была развита Эйлером, Маклореном и особенно Даниилом Бернулли. Они, не принимая в расчет движения жидкостей, рассматривали Землю как водяной вытянутый эллипсоид, постоянно находящийся в равновесии под влиянием силы тяжести и приливных сил Луны и Солнца. Эта теория статического равновесия не объясняет даже в общих чертах прилива и может служить только введением в динамическую теорию, данную Лапласом ("M écanique cé leste", книги IV и XIII). Основываясь на законах гидродинамики, Лаплас не ввел, однако, влияния трения жидкости и ввиду непреодолимых аналитических трудностей ограничился рассмотрением случая, когда океан сплошь покрывает Землю, причем глубина его изменяется в простой зависимости от широты места. Лаплас исходил из следующего основного принципа: период колебательного движения системы, в которой вследствие развившихся сопротивлений исчезли первоначальные обстоятельства движения, равен периоду сил, действующих на нее. Изложение Лапласа затемнено излишним введением шаровых функций, так что его выводы многими, например Эри, считались не вполне верными.
Эри (Airy) предложил так называемую теорию каналов. Он рассматривает действие приливной силы на очень тонкий канал, выделенный из общей массы воды. Кроме того, Эри ввел влияние трения, принимая его пропорциональным скорости. Работы Юэлла (Whewell), Лёббока (Lubbock), Ферреля и Бергена, важные по количеству собранного материала и попыткам разъяснить частности явления (см. ниже), не прибавили ничего существенного в теории. В этом отношении сделали шаг вперед Вильям Томсон и Джордж Дарвин, хотя и их главная заслуга состоит в ясном и строгом изложении теории Лапласа. Гармонический анализ прилива (см. ниже), предложенный В. Томсоном, в сущности есть эмпирический прием изображения явления. Теория приливов, несмотря на все усилия, до сих пор представляет собой первое, грубое приближение почти в том виде, какой дал ей Лаплас. Главные недостатки ее: не вводится влияние трения, а также распределения суши.
Теория приливов. Потенциал приливной силы Луны:
U = (3M/2R3) ρ 2(Cos2z — 1/3)
где z — зенитное расстояние Луны, остальные обозначения см. выше. Вызванное этой силой уклонение (ε) радиуса Земли ρ от его среднего значения a выразится при статическом равновесии формулой:
ρ = a[1 + (3Ma/2gR3){(Cos2z — 1/3)/(1 — 3/5 σ / Δ)}],
где g — ускорение силы тяжести, σ — плотность жидкой пленки (океана), Δ — плотность Земли. Делитель (1—3/5σ / Δ) выражает влияние на деформацию поверхности жидкого слоя взаимного притяжения частиц самой жидкости. Введением вместо z широты (90°—θ) и долготы (ω) места, прямого восхождения (α) и склонения (δ) светила, потенциал (а также уклонение радиуса Земли) разложится на три члена: один зависит от часового угла Луны, другой от двойного часового угла, третий не зависит от него. Если χ — действительная деформация поверхности, то динамическая теория должна объяснить разность (χ — ε). Уравнения очень малых перемещений частиц жидкости по меридиану (ξ) и параллели (η) можно написать в виде:
d2 ξ /dt2 — 2nSin θ Cos θ d η /dt = —g/a[d/d θ (χ — ε)]
Sin θ d2 η /dt2 + 2nCos θ d ξ /dt = —g/(aSin θ)(d/d ω)
где n — угловая скорость вращения Земли, а t — время. Прибавляя сюда уравнение неразрывности (см. Гидродинамика)
χ aSin θ + (d/d θ)(γξ Sin θ) + (d/d ω)(γη Sin θ) = 0
где γ глубина океана в функции от широты и долготы, и интегрируя эту систему уравнений, получим χ, ξ и η. Но точное интегрирование невозможно, даже допуская, что глубина не зависит от долготы. Остается предположить, что χ, так же как ε, выражается суммой нескольких периодических функций, то есть считать прилив составленным из отдельных волн:
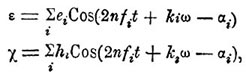
где ei и hi зависят от широты места и склонения Луны, ai от прямого восхождения, fi и ki — постоянные. Каждая разность соответственной пары амплитуд: h— е =u определится дифференциальным уравнением:
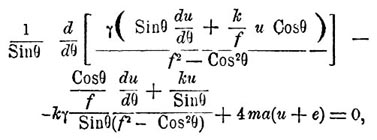
где m — отношение центробежной силы к тяжести. Но и это уравнение может быть проинтегрировано только для нескольких частных предположений. В силу основного принципа Лапласа можно ограничиться периодами, соизмеримыми с движением Луны. Лаплас рассмотрел три рода колебаний: долгого периода (зависящие лишь от склонения Луны), суточный и полусуточный (зависящие от часового угла Луны и его двойной величины). Таким образом, приливные волны имеют те же самые периоды, что и в статической теории, но амплитуды и распределение их совершенно иные. Если положить, что глубина океана уменьшается от экватора к полюсам по закону γ = l(1—qCos2 θ), где l и q постоянные, то для колебаний второго рода высота волны:
h = —[(2lq/ma)/(1—(2lq/ma))]e
т. е. для небольшой глубины динамическая теория дает почти противоположную деформацию океана, чем статическая. При q = c, то есть при постоянной глубине океана, суточные колебания совсем не существуют. Колебания третьего рода — полусуточные — наиболее значительны и не пропадают ни при каком законе распределения глубин. Если при полюсах глубина ничтожна (q = 1), а под экватором около 1/1156 радиуса Земли, то есть 5500 м, что близко к действительности, прилив совершенно обратны статическим (h = —е); во время кульминации Луны наступает отлив.
При постоянной глубине океана в 5 км полусуточные колебания могут достигнуть громадной величины, так как эта глубина соответствует их скорости распространения. Если же глубина очень велика, то они мало отличаются от статических (h = е). Амплитуда колебаний долгого периода меньше, чем дает статическая теория. Такие же колебания трех родов вызываются приливной силой Солнца. Распределение суши и неправильности дна океанов так искажают амплитуды прилива, что теоретически их вычислить невозможно, а нужно определять из наблюдений для каждой местности отдельно.
Для вычисления интерференции лунного и солнечного прилива, то есть месячного неравенства, существуют таблицы, где по аргументу — разность прямых восхождений светил — дается поправка прикладного часа, а также изменения величины прилива. Подобные таблицы с объяснением можно найти в "Annuaire du bureau des longitudes". Уже Лаплас видел, что вследствие местных условий и перемен склонения светил явление прилива настолько сложно, что для его изображения необходимо ввести много отдельных периодических функций. Эту мысль широко провел В. Томсон в своем гармоническом анализе.

Колебание взад и вперед, пропорциональное косинусу какого-нибудь равномерно растущего угла, называется гармоническим движением. Гармонический анализ состоит в разложении сложного движения на простые, гармонические. Выражение потенциалов приливных сил В. Томсон разложил в ряды, зависящие от элементов орбит Луны и Земли. На основании принципа Лапласа каждому отдельному члену разложения соответствует волна, как бы произведенная фиктивным светилом, потенциал приливной силы которого выражается взятым членом разложения. Периоды всех волн получаются теоретически, но действительное значение амплитуд и эпохи — только из наблюдений. Число таких отдельных волн В. Томсон довел до 27; из них 21 лунная, 6 солнечных. Список их всех можно найти у Hatt ("Des Marées"), также в статье Дарвина "Tides" ("Encyclopaedia Britannica"). Там даны: буквенное обозначение волны, ее название, аналитическое выражение и численное значение теоретической амплитуды, аргумент периодической функции и его изменение, т.е. величина, определяющая период волны.
Под влиянием приливной силы твердое ядро Земли также деформируется, и можно наблюдать лишь разность прилива водяной пленки — океанов и твердых приливов ядра. Если бы земной шар был сплошь из литой стали, то его стальные приливы были бы в три раза меньше, чем для водяного шара; прилив для шара из стекла составили бы 3/5 водяных. Д. Дарвин вывел из приливов долгого периода, что наблюдаемая их величина около 2/3 теоретической и поэтому твердость земного шара близка к твердости стали. Если бы Земля была эластична как резина, океанские приливы совершенно исчезли бы. То же нужно ожидать при гипотезе жидкого ядра, окруженного тонкой твердой корой. Явление прилива совершенно противоречит этой гипотезе. Вследствие океанских приливов беспрерывно перекатывается несколько тысяч кубических километров воды, что представляет громадный запас живой силы; были попытки пользоваться этой силой. Масса Луны, выведенная из наблюдений приливов, равна 1/79 массы Земли. Это число достаточно близко к другим чисто астрономическим определениям и служит поверкой теории приливов.
Наблюдения и их обработка. Для морской практики всего важнее знание момента и размера прилива. Эти величины исключительно и наблюдались в старину; затем прибавилось наблюдение отливов. Из длинного ряда подобных наблюдений, производимых в Бресте, Лаплас выводил численные коэффициенты своей теории. Такие только наблюдения — и то случайные и краткосрочные — существуют для большинства приморских местностей. Гораздо более точный способ состоит в отсчитывании через известные промежутки времени, например каждый час, уровня воды по футштоку — шесту, на котором нанесены деления. Футшток ставят в месте по возможности защищенном от волнения, разводимого ветром; его нуль определяется с помощью нивелировки относительно какого-нибудь неподвижного предмета на берегу и от времени до времени проверяется. Вместо непосредственного отсчитывания уровня пользуются поплавком, помещенным в широкой трубе, опущенной достаточно глубоко в воду. Щепочка, перекинутая через блок, соединяет поплавок с указателем, скользящим по шкале. Колебания поплавка иногда записываются автоматически и непрерывно.

С помощью того же блока и зубчатки они превращаются в горизонтальное движение штифта. Передача движения устроена так, что размеры его уменьшаются, например, в 10 раз. Мимо штифта равномерно опускается рама с листом бумаги, служащая гирей обыкновенных часов. Если бы уровень воды оставался неизменным, штифт чертил бы на бумаге прямую вертикальную линию; в зависимости же от колебаний уровня линия будет кривая. Такой прибор называется лимниграфом (maré graphe, Flutantograph, self-registering tide-gauge). Первый лимниграф был установлен в 1831 г. в Sheerness (Англия). Лимниграфы различных систем теперь имеются во многих местах. В Балтийском море 7 лимниграфов на шведском берегу, 5 — на русском (см. ниже). Середина из всех показаний инструмента за известное время называется средним уровнем моря в данном месте. Он считается нулем высот при нивелирных работах. Средний уровень может изменяться в зависимости от векового опускания или поднятия (как в Финляндии) берега. Морские глубины считаются от самого низкого уровня отливов.
Английское адмиралтейство принимало прежде для морских карт средний уровень сизигийных отливов, в последнее время принят уровень, основанный на гармоническом анализе. Кривая, записанная лимниграфом, есть результат интерференции различных приливных волн. Чтобы выделить оттуда какую-нибудь отдельную волну, нужно разбить всю кривую на промежутки, равные периоду этой волны, и просуммировать все уклонения уровня, относящиеся к одной и той же ее фазе. В среднем исключатся все посторонние волны, и останется кривая, выражающая искомую волну и волны с кратными периодами. Амплитуды этих выделенных волн находятся вычислением некоторых определенных интегралов (см. Интегральное исчисление). Для этого В. Томсон предложил употреблять специальный прибор — интегратор, изобретенный Джэмсом Томсоном (J. J. Thomson's discglobe-and-cylinder integrator). Располагая рядом нескольких таких интеграторов, приноровленных по скорости вращения их дисков к различным волнам, В. Томсон зараз находит все их амплитуды. Представив с помощью подобного гармонического анализатора (tidal harmonic analyser) прилива в каком-нибудь месте в виде ряда периодических функций, можно предсказывать моменты и величины прилива в том же месте на будущее время.
Вместо длинных вычислений В. Томсон и здесь употребляет специальный прибор (tide predictor). Нить, один конец которой укреплен неподвижно, проходит через ряд блоков; каждому из них придается гармоническое движение; периоды этих движений соответствуют периодам отдельных приливных волн. Нить суммирует все эти движения, и карандаш, прикрепленный к ее свободному концу, чертит на движущемся листе бумаги составную кривую прилива. Кривую на целый год можно получить в полчаса. Подобный инструмент функционирует в Индии; на нем 20 блоков, соответствующих двадцати главным волнам. В таблицах, издаваемых адмиралтействами разных стран, даются прикладные часы и размеры приливов для многих приморских городов. Ветер, перемены барометрического давления, дожди, таяние снегов очень сильно влияют на высоту и характер прилива. Влияние этих факторов носит название метеорологических приливов, в отличие от космических, производимых притяжением Луны и Солнца.

Результаты наблюдений. Свободному распространению волн прилива с востока на запад мешают континенты. В Тихом океане они сохраняют в среднем это направление, в Индийском распространяются с юго-востока на северо-запад, в Атлантическом с юга на север. Последний факт был доказан еще Юэллом. По его предложению в течение июня 1835 г. были произведены наблюдения на 664 станциях, расположенных на европейских и американских берегах Североатлантического океана. На основании этих и других наблюдений Лёббок и Юэлл нанесли на карту изорахии (Homopleroten, cotidal lines) — линии, соединяющие места, где приливы наступают одновременно. Изорахии, построенные Юэллом для всего земного шара, довольно гипотетичны. Вполне надежны только изорахии европейских морей и северной части Атлантического океана. Изорахии проводятся через каждый час и цифры, стоящие при них, указывают Гринвичское (обыкновенно) время прилива в дни сизигий. Чтобы получить отсюда прикладной час, нужно вычесть западную долготу места от Гринвича. В морях приливная волна — следствие океанской; направление ее зависит от проливов, через которые она вкатывается, а скорость распространения уменьшается вместе с глубиной. Приближенная формула для скорости волн: v = √(gp), где g — ускорение силы тяжести (9,8 м), а р — глубина. Чем меньше глубина моря, тем теснее расположены изорахии. В следующей таблице прикладных часов видно распространение приливной волны по северо-западным берегам Европы:
| Гибралтар |
1h47m |
Гавр |
9h18m |
| Лиссабон |
2h30m |
Булонь |
11h28m |
| Аркашон |
4h8m |
Портсмут |
11h41m |
| Брест |
3h46m |
Дувр |
11h12m |
| Ливерпуль |
11h23m |
Дюнкирхен |
12h13m |
| Дублин |
11h12m |
Остенде |
0h25m |
| Плимут |
5h37m |
Лондон |
1h53m |
| Шербург |
8h0m |
Амстердам |
3h0m |
С Остенде счет идет от новой кульминации Луны, которая отстоит от предыдущей на 12 h25m, так что прикладной час 0 h25m равносилен 12 h50m. В устьях рек приливы движутся очень медленно: так, прикладной час Антверпена = 4 h25m, Гамбурга 5 h10m, между тем как Флессингена 0 h54m, Куксхафена 0 h49m. В Северном (Немецком) море распространяются три системы волн: одна из Ла-Манша по южному берегу, другая, обогнув Шотландию, по английскому берегу с севера на юг, третья тоже с севера по норвежскому берегу. Их интерференция производит весьма сложные приливы. В открытом океане приливы очень малы. На островах Св. Елены, Вознесенья, Сандвичевых они не достигают метра. На Канарских, Ново-Гебридских — от 1 до 2 м.

Напротив, около берегов континентов приливы значительно увеличиваются и в среднем равны 4—5 м. Они достигают громадной высоты в закрытых бухтах. Самые большие — 21 м — замечены в заливе Фунди (Fundy-Bay) между Новой Шотландией и Новым Брауншвейгом. Почти таких же размеров в заливах S.-Giorge и Санта-Круц в Южной Америке. В Южно-Китайском море встречаются приливы в 11 м. Из европейских выдаются в бухте С.-Мало (Бретань) — 11 м, и около Ливерпуля — 10 м. Еще невозможно дать полное объяснение всем аномалиям приливов. В некоторых местах, например, в Гавре, полная вода длится чрезвычайно долго (что очень выгодно для морской практики) и замечаются даже два или три момента наибольшего прилива; наоборот, в Портланде — двойной отлив. Отношение между лунными и солнечными приливами меняется в широких пределах. Теоретическая его величина 2,2; Лаплас вывел для французских портов 3,0; между тем, для Фернандины (Флорида) это отношение 6,0; для Cat Island (Мексиканский залив) 1,8. Около Courtown (Ирландия), а также на островах Таити совершенно нет лунных приливов.
Суточные приливы, малозаметные в европейских морях, по ту сторону Атлантического океана довольно велики, причем их отношение к полусуточным весьма изменчиво: при входе в Мексиканский залив еще преобладают полусуточные, у Ки-Веста они равны, а у западного устья Миссисипи полусуточные ничтожны сравнительно с суточными. Большие суточные приливы у Сан-Франциско, Бомбея. В Freemantle (Западная Австралия) суточные приливы значительны часть года, а затем пропадают. Около Тонкина происходит только один прилив и один отлив в сутки. По всему Атлантическому побережью Европы возраст прилива меняется от 1 1/2 до 2 суток. Во многих американских портах он равен нулю. В Тулоне наибольшие приливы предшествуют сизигиям.

Для объяснения приливов Североатлантического океана Феррель предполагал существование между берегами Европы и Америки стоячей волны с одним узлом (см. Волны) и с периодом в 6 h12m. Под 42° северной широты между Опорто и мысом Код средняя глубина океана и его ширина довольно близко удовлетворяют условию образования такой стоячей волны, но на берегах, однако, не замечается особо больших приливов, неизбежных в этом случае. Интерференцией подобных же стоячих волн Феррель объяснял неправильности в Мексиканском заливе и у Таити. Берген, исходя из формулы для скорости волн, удачно объяснил существованием последовательных глубин — бразильской, вест-индской, североамериканской — быстрое распространение волны по берегам Америки, а также дальнейшие детали атлантических приливных волн. Он показал, что эти волны — результат интерференции двух систем, из которых главная распространяется с юга на север. Мнение Юэлла, что атлантические приливы только отражение волны, образовавшейся в Тихом океане, теперь оставлено: по всей вероятности, эти приливы не изменились бы при существовании барьера между мысами Доброй Надежды и Горн.
Во внутренних морях, как Балтийское, Черное, приливы ничтожны; вообще говоря, они являются слабыми отголосками океанских, но несомненно, что в каждом бассейне развиваются кроме того самостоятельные приливные волны; в Средиземном море около Сирта они достигают 2 м. Приливы чувствительны в озере Мичиган — сизигийные — у Чикаго 7 стм, в Millwaukee 3 стм, прикладной час 40 мин. Колебания уровня с коротким периодом от 20 до 40 мин, так называемый seiches в Женевском озере объясняются стоячими волнами, образовавшимися вследствие ударов ветра. Подобные же явления замечены в озерах Боденском, Веттер и других.

Приливы в России. Значительные и сложные приливы по сибирским берегам Тихого океана почти совершенно не изучены. Чрезвычайно большое суточное неравенство замечено у Николаевска-на-Амуре и Петропавловска. Краткосрочные наблюдения в Белом море дали для юго-западных его заливов прикладной час 5 h, а размер сизигийных приливов до 1,5 м. Более изучены незначительные приливы Балтийского моря. В Кронштадте ведутся отсчеты футштока с 1841 г. Первый лимниграф был установлен в Ганге, затем в Либаве, Петербурге и в прошлом году в Кронштадте. В Ганге еще заметна каждая приливная волна. В Кронштадте космические приливы могли быть обнаружены только в среднем из достаточного материала. Поплавок лимниграфа главной физической обсерватории в Петербурге опущен во дворе ее в колодец, который сообщается горизонтальной трубой с каналом, огибающим Масляный Буян. Обработаны данные за первые два года действия лимниграфа (1878—79). Прикладной час для Петербурга 3 h30m, лунный прилив 3 стм, солнечный 2 стм, отсюда сизигийный 5 стм и квадратурный 1 стм. Кроме того, оказалось весьма значительное суточное неравенство. В настоящее время главным гидрографическим управлением установлен в Петербурге второй лимниграф. В Черном море заметны метеорологические приливы в зависимости от таяния снегов в Южной России; они доходят до 1 3 стм.

Приливные течения. Приливы соединены неизбежно с горизонтальными передвижениями воды — приливными течениями. В открытом океане такое течение не более метра в минуту, т. е. совершенно незаметно. Около берега приливные течения имеют часто значительные скорости — несколько узлов в час; знание их очень важно в морском деле. Так как явление прилива можно рассматривать как волнообразное движение частиц воды по кругам или эллипсам (см. Волны), то в открытом море наибольшее течение соответствует полной и малой воде, а направление его меняется при среднем уровне воды, т. е. через 3 часа после отлива или прилива.
Около берегов эллипс волнообразного движения сжат и наклонен в зависимости от уклона дна, вследствие чего высшая и низшая точки его приходятся ближе к точкам перемены горизонтального движения; наконец, у самого берега течение меняется в моменты полного прилива и отлива, и поэтому часто смешивают явления приливов и приливных течений. Из наблюдений, сделанных в Port-en-Bessin, следует, что в 400 метрах от берега перемена течения наступает на час позже, чем в гавани, т. е. позже полного прилива и отлива, а в 1000 метрах — на 2 часа. Течение все еще направлено к берегу, когда вода уже значительно упала; точно так же вода стремится еще прочь от берега, между тем как уровень ее уже давно повышается. Приливные течения особенно сильны в проливах и при встрече двух систем волн. Весьма сложные и быстрые (около С.-Мало до 12 км в час) приливные течения Ла-Манша и Немецкого моря удовлетворительно объясняются теоретическими соображениями.
Сильные течения, называемые англичанами race, образуются около мысов; известен такой race вблизи Портланда. Приливные течения по берегам проливов и устьев рек меняют свое направление каждые 12 1/2 часов через все 360°. Если смотреть по распространению волны, то на левом берегу направление течения меняется по движению часовой стрелки, на правом обратно. Посреди Темзы, около Лондонского моста (London Bridge), приливное течение вверх по реке продолжается еще, когда вода уже упала на 2 фута. Подобные же явления замечаются в устьях Эльбы и других рек. Это послужило основанием ложному мнению, что приливы посреди реки наступает позже, чем у берегов. Иногда приливные течения образуют водоворот, например в Мессинском проливе (Сцилла и Харибда), в Лофотенских островах (Мальстрём). Известны приливные течения в лагунах Венеции. Ввиду важности для морской практики приливных течений часто на картах отмечаются они, а не величины самих приливов. Вообще скорость приливного течения и размеры приливов совершенно не связаны друг с другом: около Куртоуна течение достигает 7 км, а изменения уровня малы, в других же местностях Ирландии приливы более 5 метров, а течение незаметно.

Приливы в реках распространяются иногда на далекое расстояние. На реке Амазонке и ее притоках прилив чувствуется в 800 км от берега океана; вследствие медленного распространения волны на этом протяжении умещается до шести последовательных приливов. В реках часто замечается изменение формы волны. Если к устью реки подходит океанская приливная волна, изображаемая формулой HSinnt, то на основании закона скорости волн v = √gp (см. выше), распространение ее по реке выразится в первом приближении формулой: (Hsinnt)(t — x(√gp)), где x — расстояние какого-нибудь пункта по реке от устья.
Чтобы получить второе приближение, нужно обратиться к дифференциальным уравнениям движения жидкости в узком канале (см. Гидродинамика). Приближенное интегрирование их указывает на существование вторичной волны (или волны высшего порядка, over-tide) вида (AxSin2n)(t — x(√gp)), где А — постоянное. Период ее в два раза короче, а амплитуда растет с удалением от устья. Следующие приближения дают новые волны с еще более короткими периодами. Эти волны видоизменяют основную, прибыль воды происходит гораздо быстрее, чем убыль; иначе говоря, промежуток от отлива до прилива короче, чем обратно. По наблюдениям в Жиронде (Гаронна) вода прибывает и убывает:
в Pointe de Grave — 6 h10m и 6 h8m
в Pauillac — 4 h41m и 7 h37m
в Bordeaux — 3 h45m и 8 h33m
в Castets — 2 h10m и 10 h8m
В некоторых реках в зависимости от рельефа дна и других условий устья это явление имеет чрезвычайно резкий характер — прилив наступает внезапно, вода движется как бы стеной. Подобные волны высотой во много метров образуются на реке Амазонке (porroroca). Такая "ревущая" волна в некоторых реках Франции называется barre, mascaret, raz de marré e. На Сене около Quillebeuf высота маскарэ до 3 метров, скорость движения 8 метров в секунду. Эта волна еще очень велика около Кодебек, но выше по реке она исчезает. Подобное явление замечается на Ганге и нескольких реках Китая и острова Борнео. Если к устью реки подходят две океанских волны H1Sinn1t и H2Sin(n2t+ λ) с различными периодами и в разных фазах, то в реке образуются составные волны (compound-tides) с периодами, соответствующими величинам n1+n2 и n1—n2, a именно:
A(n1+n2)xSin[(n1+n2)(t—(x/√gp))+ λ ]
B(n1—n2)xSin[(n1—n2)(t—(x/√gp))+ λ ]
где A и B постоянные. Если n1 мало отличается от n2, как, например, для солнечной и лунной полусуточных волн, и при этом разность их фаз (λ) нуль, что имеет место для сизигий, то вторая из этих составных волн ничтожна, а первая совпадает со вторичной (over-tide) и усиливает ее; во время же квадратур λ = 180° и составная волна, напротив того, уменьшает размеры over-tide. Поэтому явление речных приливов должно быть резче во время сизигий, чем во время квадратур, что действительно и замечается. Важным фактором в речных приливов является еще скорость течения реки. Вторичные и составные волны вполне аналогичны высшим и комбинационным тонам в музыке. Эти волны, а поэтому и неравенство периодов убыли и прибыли воды, замечаются иногда и у морских берегов.

Воздушные приливы. Атмосфера (см. Атмосфера), окружающая нашу Землю, тоже повинуется приливной силе Луны и Солнца, но заметить эти приливы очень трудно. Они сказываются в изменении барометрического давления. Ветер, т. е. горизонтальное передвижение, совершенно незаметен. Солнечные приливы теряются в постоянном суточном колебании барометра. Существование лунных приливов доказано еще Лапласом из разбора многолетних наблюдений в Парижской обсерватории.
Приливное трение. Еще Кант в 1754 г. указал, что трение прилива может замедлить вращение Земли, иначе говоря, увеличить день. Окончательно выяснил это Делоне по поводу знаменитого спора о вековом ускорении среднего движения Луны. По вычислениям Адамса, уменьшение суток к концу каждого года составляет 0,000012 S и Земля опаздывает за столетие в своем вращении на 22 S. В новейшее время Д. Дарвин указал, какой важный космогонический фактор составляют приливы и их воздействие на вращение планет и обращение спутников.
Так как приливная волна, вообще говоря, запаздывает и не направлена прямо к Луне, то притяжение Луны, действуя на выпуклости приливного эллипсоида, стремится повернуть его обратно вращению Земли и тем замедлить это вращение. В свою очередь приливная волна действует на Луну, увеличивает время ее обращения и расстояние до Земли, так что энергия вращательного движения Земли переходит в энергию поступательного движения Луны. На основании исследований Д. Дарвина, некогда Луна и Земля почти соприкасались друг с другом, причем день — период вращения Земли — был равен месяцу — периоду обращения Луны.

Оба они не превышали четырех часов. Быть может, Луна отделилась от Земли вследствие разрыва грушевидной, указанной Пуанкаррэ, формы равновесия вращающейся жидкой массы. Вслед за тем от приливного действия день и месяц увеличивались, но сначала месяц гораздо быстрее; вместе с тем росло и расстояние между светилами. Отношение длин месяца и дня должно достигнуть известного максимума, затем уменьшиться, так как день продолжает увеличиваться и становится снова равным месяцу. Для системы Земля — Луна наибольшее отношение месяца ко дню равно 29; оно уже миновало. В то же время изменяется наклонность оси Земли (первоначально около 12°) и орбиты Луны. Побочным результатом является скручивание земного шара, чему можно видеть некоторое подтверждение в стремлении очертаний континентов и впадин океанов в северном полушарии на северо-восток, а в южном на юго-восток. Из закона замедления вращения Земли и соотношения между вращением и сжатием Дарвин вывел, что Земля отвердела менее чем 10 миллионов лет тому назад. Теория Дарвина приливного действия (tidal friction) заслуживает уже потому внимания, что ею объясняется самый странный факт в солнечной системе: быстрое обращение спутников Марса (см. Солнечная система, Системы мира).
Литература.
Полное изложение вопроса, особенно теоретической стороны, представляет статья G. Darwin: "Tides" (в "Encyclopaedia Britannica", последнее издание).
Исключительно теория приливов у Hatt, "Des Marées" ("Encyclopédie scientifique des aide-mémoire", 1895).
О гармоническом анализе, кроме Hatt, также см. Baird, "A manual for tidal observations and their reduction by the method of Harmonic Analysis" (1886);
Börgen, "Die Harmonische Analyse der Gezeitenbeobachtungen" (1885).
Элементарные объяснения и подробные сведения о деталях приливов, приливных течениях, речных приливах и т. д. можно найти у:
Boguslawski und Krümmel, "Handbuch der Ozeanographie" (том II, 1887); Attlmayr, "Handbuch der Oceanographie und Maritimen Meteorologie" (1883);
Lentz, "Flut und Ebbe und die Wirkungen des Windes auf den Meeresspiegel" (1879); Ferrel, "Tidal researches" (1874);
Comoy, "Etude pratique sur les maré es fluviales" (1881).
Статьи G. Darwin о приливных трениях помещены в "Philosophical Transactions" за 1879 и следующие годы.
Из популярных изложений лучшие: несколько устарелое в "Popul ä re Vorlesungen" von Bessel (1848) и современное в "Popular lectures and adresses" by sir W. Thomson (т. III, 1891).

При написании этого текста использовался материал из
Энциклопедического словаря Брокгауза Ф.А. и Ефрона И.А. (1890—1907).
Английский
прилив – high tide
отлив – ebb
<< Назад: Общий список терминов связанных с погодой
Рекомендуем Вам посмотреть популярные разделы сайта myvaleology.com: MENU с описанием разделов | |||
| СОЦСЕТИ | ВКЛАД | ДИЕТА | СПОРТ |
Версия all4-8 |
|||
Copyright © VZOJ 2023. Все права защищены. При перепечатке или цитировании материалов сайта myvaleology.com, пожалуйста, ставьте ссылку на сайт myvaleology.com :
<a href="https://myvaleology.com">Здоровый образ жизни</a>
Права на фотографии принадлежат их авторам.
Сайт работает на хостинге www.reg.ru , скидка на услуги по промокоду 5084-7F0E-EABE-D693
В партнерстве со www.onlinetrade.ru (Вы сразу получаете 300 Бонусов на покупки при регистрации, 1 Бонус = 1 Рубль)